Introduction
Since Abbe it's well known that the resolution of a microscope is limited by diffraction. Due to this limitation conventional optical methods are hardly applicable for nanostructured surfaces that have become standard in semiconductor industry.
Therefore, it's desirable to have a simple, non-destructive optical imaging system for creating high-resolution images in the visible domain and near infrared.
Crucial for the realization of such an optical system are the theoretical studies of V. G. Veselago [1] who proposed materials with a negative index of refraction for the first time in 1967. Using materials with a negative dielectric permittivity ε and a magnetic permeability µ the refractive index n becomes negative as well. Taking a closer look, this would result in a Poynting vector that is in the opposite direction of the wave vector and therefore the wave vector k, the magnetic field H and the electric field E yield a left-handed system (Fig. 1a).
The fields of application for metamaterials with a negative index of refraction are diverse. For our institute the optical properties of materials with a negative index of refraction are particularly interesting because they enable theoretically a perfect imaging lens [2] (Fig. 1b).
Principle of Operation
Because there are no existing materials with a negative refractive index in nature, they have to be designed and manufactured artificially. Periodical nanostructures with lattice periods well below the wavelength are one out of several options to tailor the electric and magnetic responses. For applications in the visible domain lateral sizes are in the range of 100nm.
Very promising structures are meander-type structures [3], which can act as resonators for optical wavelengths and, hence, be used to transfer evanescent near field modes to the far field. Additionally, to receive a magnified image of a sub-wavelength source, a geometrical structure has to be superimposed. Such a superstrate could be a convex surface similar to a conventional lens (Fig. 2a) or a slant surface [4]. Another option is the use of aperiodic meander structures utilizing enhanced optical transmission and resonant local field enhancement (Fig. 2b).
Optical elements that can resolve a wavelength below the diffraction limit are called "superlenses" or "hyperlenses", respectively. By the means of such a superlens a regular microscope can be used to non-destructively and without any processing resolve sub-wavelength structures.
Goals
The key to understanding the underlying physical principles of the imaging properties of metamaterial structures is the simulation of resonant interactions between excited surface waves (surface plasmon polaritons) and the electromagnetic field. Particularly suitable are rigorous methods like RCWA (Rigorous Coupled Wave Algorithm) which is utilized in Microsim, a software that was developed at our institute.
Imaging and magnifying metamaterial structures at ITO are currently a topic of research, simulation, optimization and development. Furthermore, due to the complex calculation algorithms, convergence enhancements play a major role in terms of computation time reduction (especially for structures comprised of metal).
The performance of the manufactured structures is evaluated by means of optical measurements and the retrieved parameters will be used for further improvements of the simulation. The final goal is to build a "superlens" based on nanostructure-manufacturing processes.
Superlens Results
It has been shown that surface plasmon polaritons (SPPs) propagating on the metal/dielectric interfaces of a bulk negative index material (NIM) have a dominant influence on the unique properties of these materials. Consequently, one could replace bulk NIMs by resonantly coupled surfaces that allow the propagation of SPPs [5].
A metallic meander structure (Fig. 3a) is perfectly suited as such a resonant surface due to the tunability of the short range SPP (SRSPP) and long range SPP (LRSPP) frequencies by means of geometrical variation [6].
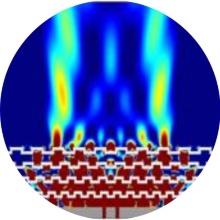
We demonstrated numerically how a stack consisting of two meander structures can mimic perfect imaging known from Pendry's lens [7] (Fig. 3b). On the other hand, to observe sub-wavelength features in the far-field more than (perfect) near-field imaging is necessary. Therefore, we have investigated stacks of meander structures with successively increasing periodicity (Fig. 4a) capable to decrease the lateral wave vector until near-field to far-field transformation is achieved (Fig. 4b). This method has been shown to work numerically and the structure seen in Fig. 4a is in the process to be fabricated at our institute via focused ion beam (FIB) milling.
References
- V.G. Veselago, "The electrodynamics of substances with simultaneously negative values of ε and μ," Sov. Phys. Usp. 10, 509 (1968).
- J.B. Pendry, "Negative Refraction Makes a Perfect Lens," Phys. Rev. Lett. 85, 3966-3969 (2000).
- L. Fu, H. Schweizer, T. Weiss, and H. Giessen, "Optical properties of metallic meanders," J. Opt. Soc. Am. B 26, B111-B119 (2009).
- A. Salandrino, N. Engheta, "Far-field subdiffraction optical microscopy using metamaterial crystals: Theory and simulations," Phys. Rev. B. 74, 075103 (2006).
- P. Alitalo, C. R. Simovski, A. Viitanen, and S. A. Tretyakov, "Near-field enhancement and subwavelength imaging in the optical region using a pair of two-dimensional arrays of metal nanospheres," Phys. Rev. B 74, 235425 (2006).
- P. Schau, K. Frenner, L. Fu, H. Schweizer, and W. Osten, "Coupling between surface plasmons and Fabry-Pérot modes in metallic double meander structures," Proc. SPIE 7711, 77111F (2010).
- P. Schau, K. Frenner, L. Fu, H. Schweizer, H. Giessen, and W. Osten, "Design of high-transmission metallic meander stacks with different grating periodicities for subwavelength-imaging applications," Opt. Express 19(4), 3627-3636 (2011).